'분류 전체보기' 카테고리의 글 목록 (11 Page)

2008. 10. 3. 21:20

하나의 끝점이 분명하게 구분이 가지 않을때..

2008. 10. 3. 21:20 in 화니 프로젝트/컬러코드

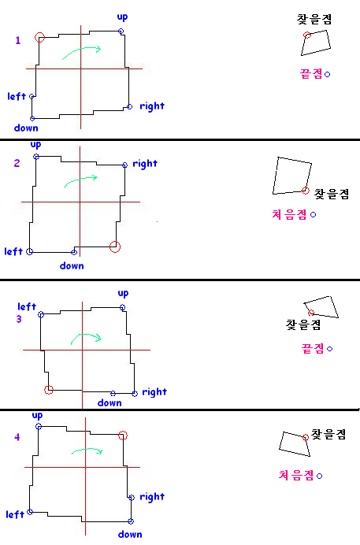
1. ⓐ 찾을 수 있는 3개의 꼭지점은 마지막 끝점을 찾아 쓴다..

ⓑ 이때 쓰는 함수는 따로 필요 없이 그대로 하면된다.

(동일된 좌표에서 마지막 좌표를 찾는 함수포함외)

ⓓ left의 x축 좌표값과 down의 x축좌표값이

같을 때로 구분할 수있다

2. ⓐ 찾을 수 있는 3개의 꼭지점은 처음점을 찾아 쓴다..

ⓑ 이때 쓰인 함수는 따로 필요하다 (소스참고)...

ⓓ left의 y축 좌표값과 down의 y축좌표값이

같을 때로 구분할 수있다.

3. ⓐ 찾을 수 있는 3개의 꼭지점은 끝점을 찾아 쓴다..

ⓑ 이때 쓰는 함수는 따로 필요 없이 그대로 하면된다.

(동일된 좌표에서 마지막 좌표를 찾는 함수포함외)

ⓓ right의 y축 좌표값과 down의 y축좌표값이

같을 때로 구분할 수있다.

4. ⓐ 찾을 수 있는 3개의 꼭지점은 처음점을 찾아 쓴다..

ⓑ 이때 쓰인 함수는 따로 필요하다 (소스참고)...

ⓓ right의 x축 좌표값과 down의 x축좌표값이

같을 때로 구분할 수있다.

기울기 구하는 거는 나중에...

------------------------------------------------------------------------------------------------------

< 구현 결과 >

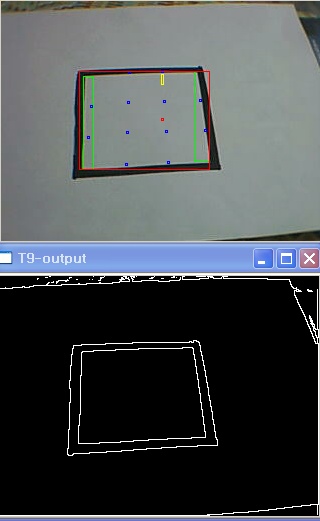
위에 보면 제대로 나온 3개의 꼭지점과는 달리 left의 좌표가

중간정도에 걸쳐 있다..현재 간단히 기울기 함수를 만들어

처리한 결과는 밑에..

이렇게 하여 left의 값이 제대로는 아니라도..

거의 근사치로 나온 것을 알수 있다..

다음은 반대방향일때

하지만 성능이 아주 안좋아...개선이 필요하다..

Posted by 깡다구짱

2008. 10. 3. 21:16

각 4개의 변들 ..중간 좌표 찾기

2008. 10. 3. 21:16 in 화니 프로젝트/컬러코드

Release-tkss8329.zip

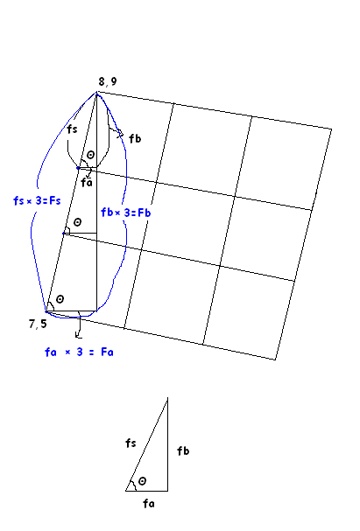
두 좌표 (8,9) 와 (7,5)사이의 기울기인 Fs는 9-5/8-7이므로

Fs는 y=ax+b에서 a=4이다..그리고 Fa는 1 Fb는 4이므로

Θ를 구할수 있다..(로테이션 소스 참고)

Fs=Fa/cosΘ 으로 구할 수 있다. Fs/3으로 각각의 fs를 구한다.

좌표는???

Fb와 Fa를 3등분한 값을 원래 Fb,Fa에서 빼고

(8,9)(7,5)를 이용하여 빼던지...더하든지..해서 3등분된 좌표를 구할 수있다..

더 정확하게 구할 수도 있지만..그리 큰 의미는 없는 거 같다.

fa=fs/cosΘ, fb=fs/sinΘ (별 의미 없는 거 같음)..ㅡㅡ

그리고..

소수점은 좌표에 존재하지 않으므로..반올림으로 처리하면

어떨까 싶다...

(7.3,6.3) -> (7,6)

(7.6,7.6) -> (8,8)

< 실제 구현 >

그냥 두 좌표에서 /3하여 원래 좌표에서... 결과값인 두 X,Y축값을
빼주어..찾음..소수점은 반올림했음..

Posted by 깡다구짱

2008. 10. 3. 21:15

아래의 방식까지..결과이미지

2008. 10. 3. 21:15 in 화니 프로젝트/컬러코드

Release-tkss8329.zip

음...

밑에 마스크 쉬운 그림선들이 짤려있는 거 같지만..

실제로는 연결되어있다..

302*240영상 패턴인식하는 동안 외곽 2,238,2,318이

넘어갈 경우에는 인식을 하지 못하도록 했다.

위에 그림을 보면 중심점이 사각형밖에 있다..그래도 패턴인식은

되는데...하다보면 y축가 240에 가까워 진다...

그걸 이용하여 238이 되면 인식이 못 되도록 했다..

양사면 모두 그런식으로 동작이 된다.

그리고 다른경우인

바깥에서 부터 인식하여 외각을 찾은 경우는

나중에 해결할 생각이다.

Posted by 깡다구짱

2008. 10. 3. 21:13

외곽선 추출 알고리즘 - 분류기

2008. 10. 3. 21:13 in 화니 프로젝트/컬러코드

Rotations()-tkss8329.zip

인식은 되는거 같은데...흠...

BOOL curer=TRUE;// 양삼면이 막힌 부분의 분류기 처림후 다음 분류기가 실행되지 않도록 하고..다시 벗어나면 TRUE로 돌림

if(b==1 && d==1 && f==1 && h==0){
  if(i==0){            // ↘
          x_move=x_move+1;
    y_move=y_move-1;
    h_r=TRUE;
    curer=FALSE;

    change_num="g01";
    if(afxmess){
    AfxMessageBox("g01");

    }
  }else if(i==1){      // ↓
          y_move=y_move-1;
          h_r=TRUE;
    curer=FALSE;

    change_num="g02";
    if(afxmess){
    AfxMessageBox("g02");

    }
  }
}else if(b==0 && d==1 && f==1 && h==1){
  if(a==0){            // ↖
          x_move=x_move-1;
    y_move=y_move+1;
    h_r=FALSE;
    curer=FALSE;

    change_num="g03";
    if(afxmess){
    AfxMessageBox("g03");

    }
  }else if(a==1){      // ↑
          y_move=y_move+1;
    h_r=FALSE;
    curer=FALSE;

    change_num="g04";
    if(afxmess){
    AfxMessageBox("g04");
    }
  }
}else if(b==1 && d==1 && h==1 && f==0){
  if(c==0){            // ↗
          x_move=x_move+1;
    y_move=y_move+1;
    h_r=TRUE;
    curer=FALSE;

     change_num="g05";
    if(afxmess){
    AfxMessageBox("g05");

    }
  }else if(c==1){      // →
          x_move=x_move+1;
    h_r=TRUE;
    curer=FALSE;

    change_num="g06";
    if(afxmess){
    AfxMessageBox("g06");

    }
  }
}else if(b==1 && d==0 && h==1 && f==1){
  if(g==0){            // ↙
          x_move=x_move-1;
    y_move=y_move-1;
    h_r=FALSE;
    curer=FALSE;

    change_num="g07";
    if(afxmess){
    AfxMessageBox("g07");

    }
  }else if(g==1){      // ←
          x_move=x_move-1;
    h_r=FALSE;
    curer=FALSE;

    change_num="g08";
    if(afxmess){
    AfxMessageBox("g08");

    }
  }
}

if(curer){

if(b==1 && c==0 && f==0){
  if(h==0){           // ↗
          x_move=x_move+1;
    y_move=y_move+1;
    h_r=TRUE;

    change_num="g09";
    if(afxmess){
    AfxMessageBox("g09");

    }
  }else if(h==1){
   if(h_r){        // ↗
              x_move=x_move+1;
        y_move=y_move+1;
        h_r=TRUE;

     change_num="g10";
     if(afxmess){
     AfxMessageBox("g10");

     }
   }else if(!h_r){
    if(g==0){   // ↙
                  x_move=x_move-1;
            y_move=y_move-1;
            h_r=FALSE;

      change_num="g11";
         if(afxmess){
      AfxMessageBox("g11");

      }
    }else if(g==1){ // ←
                  x_move=x_move-1;
            h_r=FALSE;

      change_num="g12";
      if(afxmess){
      AfxMessageBox("g12");

      }
    }
   }
  }
}else if(b==1 && c==1 && f==0){
  if(h==0){           // →
          x_move=x_move+1;
    h_r=TRUE;

     change_num="g13";
    if(afxmess){
    AfxMessageBox("g13");

    }
  }else if(h==1){     // →
   if(h_r){
              x_move=x_move+1;
        h_r=TRUE;

     change_num="g14";
     if(afxmess){
     AfxMessageBox("g14");

     }
   }else if(!h_r){ // ↙
    if(g==0){
                  x_move=x_move-1;
            y_move=y_move-1;
            h_r=FALSE;

      change_num="g15";
      if(afxmess){
      AfxMessageBox("g15");

      }
    }else if(g==1){ // ←
                  x_move=x_move-1;
            h_r=FALSE;

      change_num="g17";
      if(afxmess){
      AfxMessageBox("g17");

      }
    }
   }
  }
}

if(f==1 && h==0 && i==0){
  if(d==0){               // ↘
          x_move=x_move+1;
    y_move=y_move-1;
    h_r=TRUE;

    change_num="g18";
    if(afxmess){
    AfxMessageBox("g18");

    }
  }else if(d==1){
   if(h_r){            // ↘
              x_move=x_move+1;
        y_move=y_move-1;
        h_r=TRUE;

     change_num="g19";
     if(afxmess){
     AfxMessageBox("g19");

     }
   }else if(!h_r){
    if(a==0){       // ↖
                  x_move=x_move-1;
            y_move=y_move+1;
            h_r=FALSE;

      change_num="g20";
      if(afxmess){
      AfxMessageBox("g20");

      }
    }else if(a==1){ // ↑
                  y_move=y_move+1;
            h_r=FALSE;

      change_num="g21";
      if(afxmess){
                 AfxMessageBox("g21");

      }
    }
   }
  }
}else if(f==1 && h==0 && i==1){
  if(d==0){            // ↓
          y_move=y_move-1;
          h_r=TRUE;

    change_num="g22";
    if(afxmess){
    AfxMessageBox("g22");

    }
  }else if(d==1){
   if(h_r){         // ↓
              y_move=y_move-1;
              h_r=TRUE;

     change_num="g23";
     if(afxmess){
     AfxMessageBox("g23");

     }
   }else if(!h_r){
    if(a==0){    // ↖
                  x_move=x_move-1;
            y_move=y_move+1;
            h_r=FALSE;

      change_num="g24";
         if(afxmess){
      AfxMessageBox("g24");

      }
    }else if(a==1){ // ↑
                  y_move=y_move+1;
            h_r=FALSE;

      change_num="g25";
      if(afxmess){
      AfxMessageBox("g25");

      }
    }
   }
  }
}

if(h==1 && g==0 && d==0){
  if(b==0){            // ↙
          x_move=x_move-1;
    y_move=y_move-1;
    h_r=FALSE;

    change_num="g26";
    if(afxmess){
    AfxMessageBox("g26");

    }
  }
}else if(h==1 && g==1 && d==0){
  if(b==0){            // ←
          x_move=x_move-1;
    h_r=FALSE;

    change_num="g27";
    if(afxmess){
    AfxMessageBox("g27");

    }
  }
}

if(d==1 && a==0 && b==0){
  if(f==0){             // ↖
          x_move=x_move-1;
    y_move=y_move+1;
    h_r=FALSE;

    change_num="g28";
    if(afxmess){
    AfxMessageBox("g28");

    }
  }
}else if(d==1 && a==1 && b==0){
  if(f==0){            // ↑
          y_move=y_move+1;
    h_r=FALSE;

     change_num="g29";
    if(afxmess){
    AfxMessageBox("g29");

    }
  }
}
}

ps. 헐...소스 꼬라지 하고는..ㅡㅡ;;(2008.10월 블로그 옮기는 도중...)

Posted by 깡다구짱

2008. 10. 3. 21:11

꼭지점 좌표의 문제점①

2008. 10. 3. 21:11 in 화니 프로젝트/컬러코드

그림 1인 경우에는 시계방향으로 돌며 인식하는 패턴에 의해..

a,b,c,d 각 좌표의 끝이 마지막 배열에 저장되므로.

별로 문제될 것 없이 각 4꼭지점을 쉽게 찾을 수있다..

그러나 그림2같은 경우는 각 초록색점들이 배열에 저장되므로

위에 사진과 같이 제대로된 꼭지점을 찾지 못한다.(초록색사각형)

-> 해결방안

각 끝쪽을 찾기위해서 패턴인식하는중에 찾은 네개의 정보를

이용하였다..

먼저 배열을 4개 선언하고..

각 패턴이동시에 동작한 if문 함수(네개의 정보를 찾기 위한 소스)

에서 모든 흔적을 배열에 각각 저장하였다.

--이하 소스 참조--

// 꼭지점 찾는 소스
if(x_move>=old_x_right){

// 최고오른쪽의 꼭지점을 찾기위한 소스이지 위쪽 오른쪽 꼭지점을 찾는 소스가 아니다.
  old_x_right = x_move;
  old_x_right_y = y_move;
        ppt2[count_ppt2]=xy;
  count_ppt2++;
}else if(x_move<=old_x_left){
  old_x_left = x_move;
        old_x_left_y = y_move;
  ppt4[count_ppt4]=xy;
  count_ppt4++;
}

if(y_move>=old_y_up){
  old_y_up = y_move;
        old_y_up_x = x_move;
  ppt1[count_ppt1]=xy;
  count_ppt1++;
}else if(y_move<=old_y_down){
  old_y_down = y_move;
        old_y_down_x = x_move;
  ppt3[count_ppt3]=xy;
  count_ppt3++;
}

위에 소스중에서 if(x_move>=old_x_right){에

>=가 중요하다..=가 없다면 --------이 부분에서..

나머지 값들은 무시될수 있기 때문이다.

그럼 >만써서 처음 값만 저장하면 되지 않느냐하는

의문도 생기지만..

만약에 >로 쓰면 그림 1과 그림 2의 문제점이 바뀌어

버린다..그림2는 별 탈없이 인식이 되지만..

처음 값들만을 저장하기 때문에... 그림1과 같이 마지막

값이 필요한 경우 마찬가지로 꼭지점찾는데 문제가 생긴다..

결국엔 둘중 하나는 희생해야되는 것이다..

이렇게 저장한 배열에서 중앙y축을 기준으로 하여

old_y_up_x(제일 위쪽의 좌표-아직 완전한 꼭지점은 아님)

가 xx_half축보다 작으면 그림2와 같은 상황이 되고...소스가 동작하게 된다.

그리고 저장된 count_ppt1만큼 배열에 저장된 데이터로 부터 모든 y축 값을 뽑아네고.그 값이

old_y_up(제일 위쪽 y축값)이랑 같은 값만 if문에 실행되도록 하였다..

그러면 제일 위쪽의 ----------부분들만 처리할수 있게 된다..

이값들은 y축값은 다 같지만 x축값은 다 다르다..

이 x축 값 가운데 가장 작은 값을 찾으면..그 좌표가 바로 꼭지점이 된다.

나머지 3개의 꼭지점도 이런식으로 찾았다.

CString CColorCodeDlg::find_4points()
{
int x_x,y_y,o=0;
  CString zzz;
     if(old_y_up_x<xx_half){
            for(o; o<=count_ppt1;o++){
   y_y=Returrnsy(ppt1[o]);
            if(y_y==old_y_up){
    x_x=Returrns(ppt1[o]);
    if(result_up_x>x_x){
     result_up_x=x_x;
     old_y_up_x=x_x;
    }
   }
   }

   for(o; o<=count_ppt2;o++){
   x_x=Returrns(ppt2[o]);
            if(x_x==old_x_right){
    y_y=Returrnsy(ppt2[o]);
    if(result_right_y<y_y){
     result_right_y=y_y;
     old_x_right_y=y_y;
    }
   }
   }

   for(o; o<=count_ppt3;o++){
   y_y=Returrnsy(ppt3[o]);
            if(y_y==old_y_down){
    x_x=Returrns(ppt3[o]);
    if(result_down_x<x_x){
     result_down_x=x_x;
     old_y_down_x=x_x;
    }
   }
   }

            for(o; o<=count_ppt4;o++){
   x_x=Returrns(ppt4[o]);
            if(x_x==old_x_left){
    y_y=Returrnsy(ppt4[o]);
    if(result_left_y>y_y){
     result_left_y=y_y;
     old_x_left_y=y_y;
    }
   }
   }

}else if(old_y_up_x<xx_half){

}

  // 초기화
  result_down_x=0;
  result_left_y=240;
  result_up_x=320;
  result_right_y=0;

count_ppt1=0;
count_ppt2=0;
count_ppt3=0;
count_ppt4=0;

return "";

}

Posted by 깡다구짱

2008. 10. 3. 21:09

[펌] 각도 구하는 함수

2008. 10. 3. 21:09 in 화니 프로젝트/컬러코드

영상처리 할때 쓰일때가 많아서 이렇게 올려둡니다.

일반적으로는 중학교때 배운 수학을 떠올려보면..

tan Θ = dy / dx

라고 배웠지요. 결론,

Θ = atan( dy / dx )

이라는 선생님의 말씀. dx, dy 구해서 atan(dy/dx) 하면 나오지만

atan() 함수를 쓰지 않고 좌표 값들의 연산만으로도 각도를 구해낼 수 있더군요.

C 에서 제공해주는 atan() 함수가 테이블표에서 직접 읽어오는게 아니라면

일정 연산시간이 걸릴테고, 결국 좌표값만으로 구하는게 더 빠르다는 말씀.

1. atan() 를 써서 만든 각도 구하는 함수

double angle(int x1,int y1,int x2,int y2)
{
double dx,dy,da;

dx=x2-x1;
dy=y2-y1;

if (!dx) dx=1e-6;

da=atan(dy/dx);

if (dx<0) da+=PI;

da= da*180/PI;
return da;
}

2. atan() 를 쓰지 않고 좌표 값만으로 각도 구하는 함수

float theta(int x1, int y1, int x2, int y2)
{

int dx, dy, ax, ay;
float t;

dx = x2 - x1;
ax = abs(dx);
dy = y2 - y1;
ay = abs(dy);

t = (ax + ay == 0)?0:(float)dy/(ax+ay);

if( dx < 0 )
t = 2 - t;
else if( dy < 0 )
t = 4 + t;
return t * 90.0;
}

출처 : http://cafe.naver.com/opencv.cafe

Posted by 깡다구짱

2008. 10. 3. 21:08

Rotation 핵심 코드

2008. 10. 3. 21:08 in 화니 프로젝트/컬러코드

rotation-tkss8329.zip

○ 원래는 빨간영역부분만 기준점으로 쓸려고 했으나...

그러면..만약 다른 모서리부분이 또한 빨간색을 뛰게 되면

기준점을 알수가 없다..

그래서..레드, 블랙, 그린을 3가지의 모서리 기준점을 두었다..

○ 양쪽 모서리 부분의 위치를 정확히 알아내는것이 너무

난해하여...로테이션작업후에도..좀 삐뚤어져 있는 현상도

있었으며...코드자체도 상당히 길었다...

○ 맨위의 그림처럼 모서리가 빨간 부분을 위쪽..그리고 왼쪽이라

정하고...나머리..2개의 모서리에 있는 색을 구분하여..

+90,+180,+270를 더해주어 정확한 칼라코드의 모양을 나타내었다..

○ 로테이션 각도는 tanΘ=dy/dx를 이용하여...기울어진 Θ를

구하였고...dx 와 dy 값은 인식한 원본 칼라코드의

각각 변들의 끝점을 칼라인식하여..배열에 넣어둔 뒤에..

결정된 칼러가 가지고 있는 배열안의 위치좌표를

뽑아내었다..

그 칼라가 위치하는 좌표를 를 전체변의 길이와 뺀 값을 이용이 dx와 dy이다.

문제점 : 앞에서 말한 것과 같이 dx와 dy의 정확한 위치를

잘 못잡아내어..로테이션후의 처리된 컬러코드도

많이 삐뚤거나..아예 다이아몬드처럼 나온경우도

있었다...

물론 내가 실험에 쓴 컬러코드를 대충그린 것도

원인이 되겠지만..인식률을 높이기 위해서..

이런 것들과 다 극복해 낼 필요가 있다..

참고 : 로테이션 함수인 GetQuadrangeSubPix()는 카페에서

제공한 라이브러리에는 포함되어있지 않은 것 같아..

다른 라이브러리를 가져다 썼다.

Posted by 깡다구짱

2008. 10. 3. 21:07

컬러코드 생성기 기초 제작

2008. 10. 3. 21:07 in 화니 프로젝트/컬러코드

자체 제작했음..

Release-tkss8329.zip

구현방법 : OpenCv

데이터베이스가 아닌 일단 배열로 저장을 했고...

저장용량은 연습삼아..한 10개정도만...

그리고

3Ⅹ3 매트릭스를 기준으로 만들었다...

각각 색을 채우는 것은 각 영역의 좌표를 구한뒤에..

(따로 함수가 있을 거 같은데..못 찾아서...)

그 좌표를 조금씩 줄이고..늘려가면서..

사각형을 그려 채웠다...

거의 확률은 적겠지만..랜덤하게 만들어지는 색의 중복을

제어하기 위한 소스도 넣었고...

나중에..데이터베이스개념으로만 바뀌면 될듯하다..

Posted by 깡다구짱

2008. 10. 3. 21:06

rotation문제

2008. 10. 3. 21:06 in 화니 프로젝트/컬러코드

컴퓨터 캠으로 인식하기 때문에...

rotation문제가 좀 그렇다...

그냥 최대한 인식을 한 컬러코드의 매트릭스

전체 이미지를 25영역으로 나누어..바로 색을

인식하던가..

아니면 인식한 것을 다시 정사각형의 가상 매트릭스에

넣어 처리하던가...근데...

다시 넣는 거는 거의 무의미 할꺼 같다.ㅡㅁㅡ

아무튼...인식할 때가 제일 문제인데..

첫째, 인식하는 알고리즘을 짤 때 무엇을 기준으로

패턴을 인식시켜 학습시키는 지가 문제인거 같다...

rotation되어 있는 거까지 인식한다는 것은

얼굴인식에서..옆모습도

인식을 하게 한다는거랑 똑같은거다...ㅡㅁㅡ

꽤 난이도가 있을 듯...

둘째, 인식을 한다고 해도..그 영역을 어떻게 가져오는냐다..

보통 얼굴인식이나...사물인식을 보면 사각 rect형태로 되어

인식한 이미지를 가져 왔는데..

만약 사다리꼴형태로 되어있다면

사다리꼴 밑부분의 좌표를

기준으로 인식부분을 사각형을 그려야 한다는 것인가???

그리고...사다리꼴의 윗면 첫 좌표도 가지고 와서..

컬러인식할 때...사다리꼴에 맞쳐 분활하여 인식하여야 하나??

그림 1-1(밑에) 처럼 말이다..

그리고 그림2-1의 경우가 가장 많이 발생할 것으로 보이는데..

이 경우 흠....

처음부터 전체 원본 이미지를 회전시켜서 가지고 오느냐?

아니면..바로 가져올 수 있는 방법이 있을까?? 패턴인식 알고리즘

만들 때 같이 구현해야하나??

알고리즘을 따로 만들어야 할 듯하다..패턴인식알고리즘안에

같이 만들던지...ㅡㅁㅡ

..

아니지..패턴인식하는 알고리즘에서 다 넣어야 되네..^^

그러니까 알고리즘이지....ㅡㅡ

Posted by 깡다구짱

2008. 10. 3. 21:04

표준화 문제

2008. 10. 3. 21:04 in 화니 프로젝트/컬러코드

현재 컬러코드의 작성 표준화가 아무곳에도 나와 있지 않다..

다만..위 사진으로 보아...D11~D44와 P1r.c..그리고 Pra가

있다...P1r.c...은 각각 4가지 색을 기본으로 하여..

4개영역...총 256개의 정보를 저장한다...

....

물론 25개 영역을 모두 사용하면 그 양은 엄청나겠지만..

그렇게 되면 표준화의 의미가 없어지고..검색이 어려우러 것이다.

..

자료에 보면 5×5 매트릭스의 경우 표현 가능한 주소공간이

32비트로 40억개 이상의 데이터를 관리한다고 했다..

위에 처럼 D11~D44까지 총 16개 영역을 4개 색깔로 표현하니까.

4*4*4*4*4*4*4*4*~~~해서 총 16번 곱하면 된다..

그럼 값은..4294978296..약 42억으로 위에 내용과 맞아 떨어진다..

또 다양한 매핑(mapping) 기법을 도입하면 170억개 데이터까지

확장이 가능하다고 했는데..

이건 아마도 다른 영역과는 관련이 없는거 같다...아니면

위에 그림과 달리..

조금 형태를 바꾸는 것을 말하는 것일지도 모른다.

그럼 나머지 영역은 뭐를 뜻하는 걸까??

제품의 종류?...국가?...등급?..을 뜻하는 것일 텐데..

그럼 먼저 인식한 값을 이진화나..아니면 다른 실수형?정수형?의

숫자 나타내고..그 값을 토대로..DB가 이 나머지 영역의 정보를

이용하여 좀더 신속하게...찾을 수 있을 것이다..

40억개나 하는 정보를 어느 세월에 검색하겠나..??..

어떤 방식으로 되어있지???? 좀 더 찾아 봐야 할꺼 같다..

Posted by 깡다구짱

…·─━☆ 무한코딩세계

'분류 전체보기'에 해당되는 글 174건

하나의 끝점이 분명하게 구분이 가지 않을때..

각 4개의 변들 ..중간 좌표 찾기

아래의 방식까지..결과이미지

외곽선 추출 알고리즘 - 분류기

꼭지점 좌표의 문제점①

[펌] 각도 구하는 함수

Rotation 핵심 코드

컬러코드 생성기 기초 제작

rotation문제

표준화 문제

Category

Tag Cloud

My Link

Notice

Recent Article

Recent Comment

티스토리툴바